B3. Act. 15. Sucesión numérica. 17/1/17
Tema. Cómo obtener una regla o fórmula para una sucesión numérica.
Una sucesión es un conjunto de cosas (normalmente números) una detrás de otra, en un cierto orden.
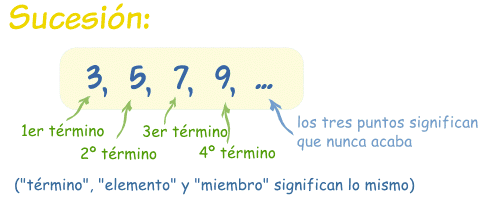La regla
Una sucesión sigue una regla que te dice cómo calcular el valor de cada término.
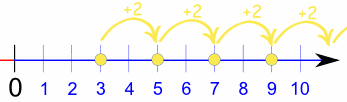
Ejemplo: la sucesión {3, 5, 7, 9, ...} empieza por 3 y salta 2 cada vez:
¡Pero la regla debería ser una fórmula!
Decir que "empieza por 3 y salta 2 cada vez" no nos dice cómo se calcula el:
- 10º término,
- 100º término, o
- n-ésimo término (donde n puede ser cualquier número positivo que queramos).
Así que queremos una fórmula con "n" dentro (donde n será la posición que tiene el término).
Entonces, ¿cuál sería la regla para {3, 5, 7, 9, ...}?
Primero, vemos que la sucesión sube 2 cada vez, así que podemos adivinar que la regla va a ser "2 × n". Vamos a verlo:
Probamos la regla: 2n
| n | Término | Prueba |
|---|
| 1 | 3 | 2n = 2×1 = 2 |
| 2 | 5 | 2n = 2×2 = 4 |
| 3 | 7 | 2n = 2×3 = 6 |
Esto casi funciona... pero la regla da todo el tiempo valores 1 unidad menos de lo que debería, así que vamos a cambiarla un poco:
Probamos la regla: 2n+1
| n | Término | Regla |
|---|
| 1 | 3 | 2n+1 = 2×1 + 1 = 3 |
| 2 | 5 | 2n+1 = 2×2 + 1 = 5 |
| 3 | 7 | 2n+1 = 2×3 + 1 = 7 |
¡Funciona!
Así que en vez de decir "empieza por 3 y salta 2 cada vez" escribimos la regla como
La regla para {3, 5, 7, 9, ...} es: 2n+1
Ahora, por ejemplo, podemos calcular el término 100º: 2 × 100 + 1 = 201
Notación
Para que sea más fácil escribir las reglas, normalmente lo hacemos así:
|
Posición del término
|
 |
Es normal usar xn para los términos:
- xn es el término
- n es la posición de ese término
|
| Así que para hablar del "quinto término" sólo tienes que escribir: x5 |
Entonces podemos escribir la regla para {3, 5, 7, 9, ...} en forma de ecuación, así:
xn = 2n+1
Ahora, si queremos calcular el 10º término, podemos escribir:
x10 = 2n+1 = 2×10+1 = 21
¿Puedes calcular el 50º término? ¿Y el 500º?
Actividad. Utiliza las siguientes reglas para calcular las posiciones 1, 2, 5, 9, 12 y 21.
1n+3
2n-6
2n+7
11n+5
16n+9
12n-4
8n+3
-6n+6
-7n+10
-5n+4
-4n-10
-8n-14
