Actividad. Elabora el formulario de los temas:
- Simetría axial.
- Simetría central.
- Teorema de Pitágoras (lado c).
- Teorema de Pitágoras (lado b).
- Teorema de Pitágoras (lado a).
miércoles, 26 de octubre de 2016
B2. Act. 10. Formulario. 27/10/16
B2. Act. 10. Formulario. 27/10/16
Actividad. Elabora el formulario de los temas:
Actividad. Elabora el formulario de los temas:
B2. Act. 9. Teorema de Pitágoras. 26/10/16
B2. Act. 9. Teorema de Pitágoras. 26/10/16
Cálculo de a.
Los pasos son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de a.
Ejemplo.
Cuál será la medida del lado A en el siguiente caso.
La fórmula que se utiliza en este caso es:
a²=c²-b²
Sustituimos los datos en la fórmula:
a²=5²-4²
Resolvemos respetando la jerarquía de operaciones:
a²=25 - 16
a²=9
En el siguiente paso el cuadrado de la letra b pasa de lado contrario como una raíz cuadrada quedando así:
a=√9
a=3
Actividad. Calcular el lado a, para cada una de las siguientes situaciones , observa las medidas.
Cálculo de a.
Los pasos son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de a.
Ejemplo.
Cuál será la medida del lado A en el siguiente caso.
La fórmula que se utiliza en este caso es:
a²=c²-b²
Sustituimos los datos en la fórmula:
a²=5²-4²
Resolvemos respetando la jerarquía de operaciones:
a²=25 - 16
a²=9
En el siguiente paso el cuadrado de la letra b pasa de lado contrario como una raíz cuadrada quedando así:
a=√9
a=3
Actividad. Calcular el lado a, para cada una de las siguientes situaciones , observa las medidas.
B2. Act. 8. Teorema de Pitágoras. 25/10/16
B2. Act. 8. Teorema de Pitágoras. 25/10/16
Cálculo de b.
Los pasos son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de b.
Ejemplo.
Cuál será la medida del lado B en el siguiente caso.
La fórmula que se utiliza en este caso es:
b²=c²-a²
Sustituimos los datos en la fórmula:
b²=5²-3²
Resolvemos respetando la jerarquía de operaciones:
b²=25 - 9
b²=16
En el siguiente paso el cuadrado de la letra b pasa de lado contrario como una raíz cuadrada quedando así:
b=√16
b=4
Actividad. Calcular el lado b, para cada una de las siguientes situaciones , observa las medidas.
Cálculo de b.
Los pasos son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de b.
Ejemplo.
Cuál será la medida del lado B en el siguiente caso.
La fórmula que se utiliza en este caso es:
b²=c²-a²
Sustituimos los datos en la fórmula:
b²=5²-3²
Resolvemos respetando la jerarquía de operaciones:
b²=25 - 9
b²=16
En el siguiente paso el cuadrado de la letra b pasa de lado contrario como una raíz cuadrada quedando así:
b=√16
b=4
Actividad. Calcular el lado b, para cada una de las siguientes situaciones , observa las medidas.
B2. Act. 7. Teorema de Pitágoras. 24/10/16
B2. Act. 7. Teorema de Pitágoras. 24/10/16
Tema. Teorema de Pitágoras.
Este teorema se utiliza para calcular la longitud de uno de los lados de un triángulo rectángulo, sólo se puede utilizar en este tipo de triángulos.
Sus lados se representan con letras:
La letra a corresponde al lado más pequeño.
La letra b al lado mediano.
La letra c al lado más largo.
La fórmula qué se utiliza dependerá del lado solicitado.
Los pasos para obtener alguno de sus lados son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de c.
Ejemplo.
Cuál será la medida del lado C en el siguiente caso.
La fórmula que se utiliza en este caso es:
c²=a²+b²
Sustituimos los datos en la fórmula:
c²=3²+4²
Resolvemos respetando la jerarquía de operaciones:
c²=9+16
c²=25
En el siguiente paso el cuadrado de la letra c pasa de lado contrario como una raíz cuadrada quedando así:
c=√25
c=5.
Actividad. Calcular el lado c, para cada una de las siguientes situaciones , observa las medidas.
Tema. Teorema de Pitágoras.
Este teorema se utiliza para calcular la longitud de uno de los lados de un triángulo rectángulo, sólo se puede utilizar en este tipo de triángulos.
Sus lados se representan con letras:
La letra a corresponde al lado más pequeño.
La letra b al lado mediano.
La letra c al lado más largo.
La fórmula qué se utiliza dependerá del lado solicitado.
Los pasos para obtener alguno de sus lados son:
1. Se anota la fórmula de acuerdo al lado faltante.
2. Se sustituyen los valores en la fórmula.
3. Se resuelven las operaciones respetando la jerarquía, el resultado corresponderá a la medida del lado faltante.
Cálculo de c.
Ejemplo.
Cuál será la medida del lado C en el siguiente caso.
La fórmula que se utiliza en este caso es:
c²=a²+b²
Sustituimos los datos en la fórmula:
c²=3²+4²
Resolvemos respetando la jerarquía de operaciones:
c²=9+16
c²=25
En el siguiente paso el cuadrado de la letra c pasa de lado contrario como una raíz cuadrada quedando así:
c=√25
c=5.
Actividad. Calcular el lado c, para cada una de las siguientes situaciones , observa las medidas.
B2. Act. 6. Simetría central. 20/10/16
B2. Act. 6. Simetría central. 20/10/16
Tema. Simetría central.
Actividad. Crea en tu cuaderno 5 figuras a las que apliques la simetría axial y 6 figuras a las que apliques la simetría central.
Tema. Simetría central.
Una simetría central, de centro el punto O, es un movimiento del plano con el que a cada punto P del plano le hace corresponder otro punto P', siendo O el punto medio del segmento de extremos P y P'.
Para crear una figura y aplicar simetría central se debe considerar lo siguiente:
1 crea la figura original
2 marca el centro de simetría en cualquier espacio
3 mide la distancia que existe entre cada vértice hacia el centro de simetría
4 traza las líneas correspondientes desde el centro de simetría hacia la figura simétrica
nota marca los vértices de la figura simétrica con letras y el número 1 ya que indican que esa es la figura copiada, observa el ejemplo.
Para crear una figura y aplicar simetría central se debe considerar lo siguiente:
1 crea la figura original
2 marca el centro de simetría en cualquier espacio
3 mide la distancia que existe entre cada vértice hacia el centro de simetría
4 traza las líneas correspondientes desde el centro de simetría hacia la figura simétrica
nota marca los vértices de la figura simétrica con letras y el número 1 ya que indican que esa es la figura copiada, observa el ejemplo.
B2. Act. 5. Simetría axial. 20/10/16
B2. Act. 5. Simetría axial. 20/10/16
Tema. Simetría axial o reflectiva.
La simetría axial o reflectiva (a veces llamada simetría bilateral o simetría especular) se reconoce fácilmente, porque una mitad es el reflejo de la otra.
En este tipo de simetría se utiliza un eje que es una línea recta para crear la figura simétrica.
Podemos apoyarnos de un plano cartesiano para que la figura resulte exacta.
Actividad. Crea 5 figuras a las que apliques la simetría axial. Recuerda colocar las letras de los vértices.
Tema. Simetría axial o reflectiva.
La simetría axial o reflectiva (a veces llamada simetría bilateral o simetría especular) se reconoce fácilmente, porque una mitad es el reflejo de la otra.
En este tipo de simetría se utiliza un eje que es una línea recta para crear la figura simétrica.
Podemos apoyarnos de un plano cartesiano para que la figura resulte exacta.
 |
La cara de mi perro "Flame" es perfectamente simétrica, después de retocar un poco la foto.
La línea blanca del centro se llama eje de simetría
|
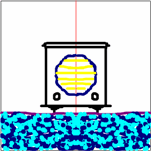
El reflejo en este lago también tiene simetría, pero en este caso:
|  |
Eje de simetría
 |
El eje de simetría (también llamado eje especular) no tiene por qué ser vertical ni horizontal, puede ir en cualquier dirección.
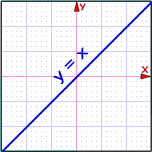
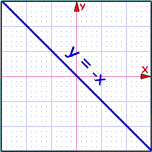
Pero hay cuatro direcciones comunes, sus nombres vienen de las líneas que denotan en un gráfico estándar XY.
Mira estos ejemplos (los dibujos están hechos con el Artista de simetría)
|
Eje de simetría
|
Ejemplo de arte
|
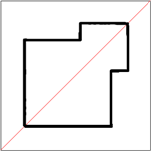
Ejemplo de forma
|
 |  |  |
 |  |  |
 |  |  |
 |  |  |
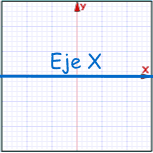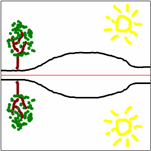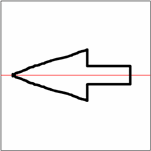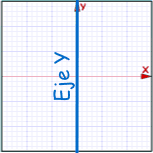Actividad. Crea 5 figuras a las que apliques la simetría axial. Recuerda colocar las letras de los vértices.
martes, 18 de octubre de 2016
B2. Act. 4. Encuesta. 18/10/16
B2. Act. 4. Encuesta. 18/10/16
Actividad. Aplica a 16 personas las preguntas que elaboraste en la sesión anterior. Recuerda elaborar una tabla donde regístrese las respuestas.
Actividad. Aplica a 16 personas las preguntas que elaboraste en la sesión anterior. Recuerda elaborar una tabla donde regístrese las respuestas.
B2. Act. 3. Encuesta. 17/10/16
B2. Act. 3. Encuesta. 17/10/16
Tema. Encuesta
La encuesta es una serie de preguntas, que pueden ser abiertas o cerradas, y se utilizan para recabar datos de determinada temática.
Preguntas abiertas.
Estas preguntas no tienen opciones de respuesta y le permiten al encuestado expresar su opinión de forma amplia.
Este tipo de preguntas pueden presentar una dificultad, ya que al momento de concentrar la información y representarla se tienen que crear categorías para ubicar la respuesta de cada uno de los encuestados.
Normalmente este tipo de preguntas se utilizan para identificar la percepción, de forma amplia, que tienen los encuestados en relación a ciertas temáticas.
Ejemplo.
¿Qué opinas de la seguridad en tu país?
Preguntas cerradas.
Este tipo de preguntas tienen respuestas predeterminadas la cantidades de opciones en las respuestas pueden variar.
La ventaja de este tipo de preguntas es que la información se puede sistematizar y manipular fácilmente. La desventaja es que podría no revelar la opinión real determinado tema.
Ejemplo.
¿ Qué color de ropa te gusta más?
A) azul. B) rojo. C)negro. D) blanco.
Actividad. Elabora 8 preguntas cerradas del tema que desees. Puede realizarse individual, en parejas o tercias. Debe aplicarse a 16 personas
Tema. Encuesta
La encuesta es una serie de preguntas, que pueden ser abiertas o cerradas, y se utilizan para recabar datos de determinada temática.
Preguntas abiertas.
Estas preguntas no tienen opciones de respuesta y le permiten al encuestado expresar su opinión de forma amplia.
Este tipo de preguntas pueden presentar una dificultad, ya que al momento de concentrar la información y representarla se tienen que crear categorías para ubicar la respuesta de cada uno de los encuestados.
Normalmente este tipo de preguntas se utilizan para identificar la percepción, de forma amplia, que tienen los encuestados en relación a ciertas temáticas.
Ejemplo.
¿Qué opinas de la seguridad en tu país?
Preguntas cerradas.
Este tipo de preguntas tienen respuestas predeterminadas la cantidades de opciones en las respuestas pueden variar.
La ventaja de este tipo de preguntas es que la información se puede sistematizar y manipular fácilmente. La desventaja es que podría no revelar la opinión real determinado tema.
Ejemplo.
¿ Qué color de ropa te gusta más?
A) azul. B) rojo. C)negro. D) blanco.
Actividad. Elabora 8 preguntas cerradas del tema que desees. Puede realizarse individual, en parejas o tercias. Debe aplicarse a 16 personas
B2. Act. 2. Examen. 17/10/16
B2. Act. 2. Examen. 17/10/16
Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.
Actividad. Examen pegado en el cuaderno y firmado por el padre o tutor.
B2. Act. 1. Carátula. 14/10/16
B2. Act. 1. Carátula. 14/10/16
Actividad. Elabora la carátula correspondiente al segundo bimestre. Los datos que debe tener son:
Nombre.
Grado.
Grupo.
Dibujo relacionado a las festividades del bimestre.
Actividad. Elabora la carátula correspondiente al segundo bimestre. Los datos que debe tener son:
Nombre.
Grado.
Grupo.
Dibujo relacionado a las festividades del bimestre.
miércoles, 5 de octubre de 2016
B1. Act. 30. Retroalimentación 5/10/16
B1. Act. 30. Retroalimentación 5/10/16
Actividad. Resuelve las páginas 22, 23, 24 y 25 de tu libro. Si tienes dudas revisa las anotaciones y ejercicios de tu cuaderno.
Actividad. Resuelve las páginas 22, 23, 24 y 25 de tu libro. Si tienes dudas revisa las anotaciones y ejercicios de tu cuaderno.
B1. Act. 29. Retroalimentación 4/10/16
B1. Act. 29. Retroalimentación 4/10/16
Actividad. Resuelve las páginas 18, 19, 20 y 21 de tu libro. Si tienes dudas revisa las anotaciones y ejercicios de tu cuaderno.
Actividad. Resuelve las páginas 18, 19, 20 y 21 de tu libro. Si tienes dudas revisa las anotaciones y ejercicios de tu cuaderno.
lunes, 3 de octubre de 2016
B1. Act. 28. Probabilidad. 29/9/16
B1. Act. 28. Probabilidad. 29/9/16
Actividad. Analiza las siguientes situaciones y calcula la probabilidad en fracción, decimal y porcentaje. Crea las tablas correspondientes para organizar la información.
Rebeca tiene una bolsa 20 pelotas azules, 30 amarillas, 8 verdes, 15 moradas, 5 rosas y 60 blancas. ¿Cuál sería la probabilidad para cada color si eligiera al azar?
En una tlapaleria venden 5 tablas de perfoacel, 5 desarmadores, 5 focos, 8 clavos y 7 soquet ¿Cuál sería la probabilidad para cada color si eligiera al azar?
En una verdulería venden 16 zanahorias, 34 jitomates, 45 cebollas, 105 ajos y 3 aguacates
¿Cuál sería la probabilidad para cada color si eligiera al azar?
Actividad. Analiza las siguientes situaciones y calcula la probabilidad en fracción, decimal y porcentaje. Crea las tablas correspondientes para organizar la información.
Rebeca tiene una bolsa 20 pelotas azules, 30 amarillas, 8 verdes, 15 moradas, 5 rosas y 60 blancas. ¿Cuál sería la probabilidad para cada color si eligiera al azar?
En una tlapaleria venden 5 tablas de perfoacel, 5 desarmadores, 5 focos, 8 clavos y 7 soquet ¿Cuál sería la probabilidad para cada color si eligiera al azar?
En una verdulería venden 16 zanahorias, 34 jitomates, 45 cebollas, 105 ajos y 3 aguacates
¿Cuál sería la probabilidad para cada color si eligiera al azar?
Suscribirse a:
Entradas (Atom)